
Bu sayfadaki her öğe bir House Beautiful editörü tarafından seçildi. Satın almayı seçtiğiniz bazı ürünler için komisyon kazanabiliriz.
Oldukça fazla bir şey yok sinir bozucu matematik problemi, zihin büken optik illüzyonveya bükülen mantık bulmacası tüm üretkenliği durdurmak için Popüler Mekanik ofis. İnsanları doğaları gereği merak ediyoruz, ama aynı zamanda inatçı bir ısrarla paylaşıyoruz. doğru, kahretsinve böylece görünüşte mümkün olan birkaç çözümle ilgili bir sorunla karşılaştığımızda işi yol kenarına atma eğilimindeyiz.
Bu üçgen zeka oyunu yeni değil; Popsugar için ortaya çıkarmak birkaç yıl önce — ama bazı gölgeli İnternet büyüsüne dayanarak, aşağıdaki tweet bugün beslememde tekrar ortaya çıktı ve personel genelinde yeni bir tartışmaya başladı Slack kanalı, geleneksel olarak atölye fikirleri için ayrılmış, ancak bunun yerine çoğunlukla ara sıra dönüştüğümüz diğer şeyler hakkında bağırmak için kullanılan bir yer içeriği.
Söyle? pic.twitter.com/lrhXrWw5EP
- J (@jiteshpillaai) Instagram Profilini Görüntüle 9 Nisan 2018
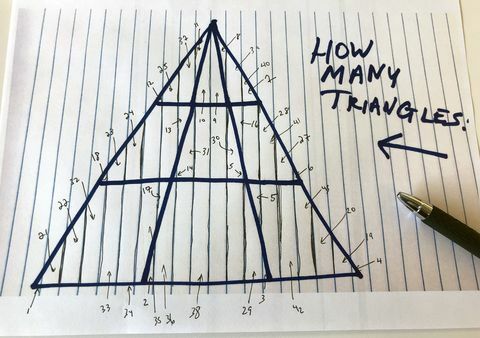
Ben bir mazoşist olduğum için, üçgeni tekrar çizdim ve personelden herkesten derhal yaptıklarını bırakmasını ve basit soruyu çözmeye çalışmasını istedim: Kaç üçgen bulabilirsin?
Size tüm sohbeti yedekleyeceğim - güven bana, kimse bunu görmek istemiyor - ama ekibin tepkileri her yerde değişiyordu. Bazı editörler dört üçgen gördü. Diğerleri 12 gördü. Bazıları 6, 16, 22 gördü. Daha da fazlası 18. Bir bilge, sorunun kendisinde bulunan A'ların üçgenlerini sayarken, bir diğeri varoluşsal görünüyordu kriz: “Bu çizgilerin hiçbiri gerçekten düz değil, sadece eğriler — böylece hiçbirini üçgen olarak tanımlayamazsınız” dedim. “Bu fotoğrafta üçgen yok. Hayatın bir anlamı yok. ”
Daha sonra sorunu 5 ila 14'ten 37'ye kadar cevapları da gamut kullanan Instagram takipçilerimize sunduk. Burada trol kullanma olasılığının yüksek olduğunu kabul etsek de, insanların soruna birçok farklı şekilde yanıt verdiği açıktır.
Instagram'da bu yayını görüntüle
Lütfen yaptığınız işi durdurun ve ofiste yaptığımız bir tartışmayı çözmemize yardımcı olun. Burada kaç tane üçgen görüyorsun?
Tarafından paylaşılan bir yayın Popüler Mekanik Dergisi (@popularmechanics) tarihinde
Meslektaşlarımı tüm gün şüpheli süreçlerini açıklarken dinleyebilirdim, ancak bunun yerine, bir fikir birliğine ulaşıp ulaşamayacağımızı görmek için birkaç geometri uzmanına ulaştım. Neredeyse temas kurduğum matematikçilerin hepsi aynı çözümü buldu - ama hepsi aynı şekilde çözemedi.
Cevabı henüz bilmek istemiyorsanız, okumayı bırakın ve önce sorunu çözmeye çalışın. İşiniz bittiğinde sizinle tekrar buluşacağım.
Hey, çabuk oldu. Cevap için hazır mısınız? Bazılarının aksine viral matematik problemleri kasıtlı olarak belirsiz ve yoruma açık olan, bunun aslında slam-dunk, şüphesiz bir çözümü var ve 18. Neden geometri uzmanlarından bazılarını duyalım.
“Buna herhangi bir matematiksel probleme yaklaşır gibi yaklaşırdım: azaltın ve yapı bulun,” diyor Sylvester Eriksson-Bique, Kaliforniya Üniversitesi Los Angeles’ın matematik dalında doktora sonrası araştırmacı Bölüm.
Erikkson-Bisque, çizdiğim şekilde üçgen oluşturmanın tek yolunun, üst tepe noktasının (köşe) üçgenin bir parçası olup olmadığıdır. Üçgenin tabanı aşağıdaki üç seviyeden biri olmalıdır. “Üç seviye vardır ve her birinde altı farklı yoldan bir temel seçebilirsiniz. Bu 18 veya 3 kez 6 üçgen verir. ”
Şimdi ana üçgene bakalım.
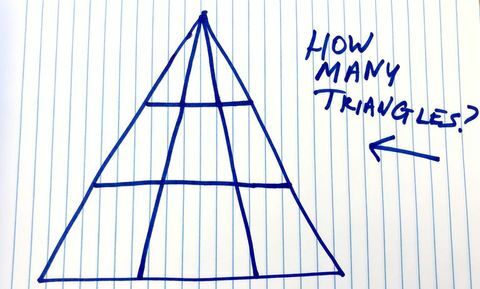
Andrew Daniels
“Davanın olduğu davaya genelleme yapmak uygun n üst tepe noktasından geçen çizgiler ve p yatay çizgiler, ”diyor Güney Kaliforniya Üniversitesi'nde matematik profesörü olan Francis Bonahon.
Bizim durumumuzda, n = 4 ve p = 3. Çizimde bulduğumuz herhangi bir üçgenin bir üst tepe noktası ve iki tanesi aynı yatay çizgide olmalıdır, bu nedenle her yatay çizgi için üçgen sayısı bu satırdaki iki köşe, bu köşe noktalarını seçebileceğimiz yol sayısına eşittir, diyor Bonahon - iki farklı noktadan birini seçebilmemiz için nveya “n 2'yi seçin. ”
Lise matematik hatırlıyor musun? Yani en n(n-1)/2. Ve orada olduğundan p yatay çizgiler, diyor Bonahan, bu verir p n(N-1) / 2 olası üçgen. Bizim durumumuzda, bu 3x4 (4-1) / 2 = 18.
Aşağıda olası her üçgeni nasıl bulacağınıza dair kullanışlı bir döküm:
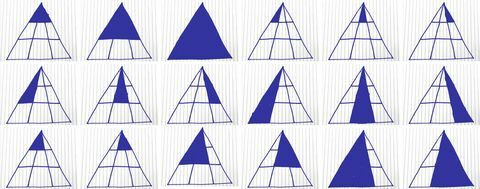
Kory Kennedy
Buffalo Üniversitesi'nde matematik yardımcısı öğretim üyesi yardımcısı Johanna Mangahas da 18'e geldi - önce basit kaba kuvvet sayımı, sonra aynı kurnazlık yoluyla yukarıdaki gibi kominatorikler - ancak üçgen beyin teaser'ımızın, Carnegie Mellon Üniversitesi'ndeki matematik profesörü Po-Shen Loh'dan bu kadar güzel olmadığını itiraf ediyor. Pittsburgh, olduğu gibi özellikli New York Timesgeçen yıl:
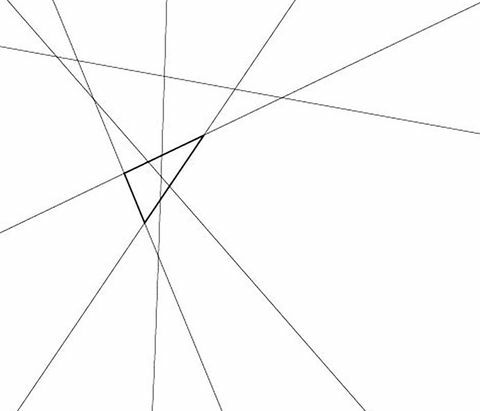
Po-Shen Loh
Bunun daha matematiksel bir cevabı var, çünkü burada üçgen saymak, altı arasından seçilen üç çizginin kombinasyonlarını saymakla aynı şeydir [6-select-3 = (6 * 5 * 4) / (3 * 2 * 1)].
“Bu durumda, her çizgi çifti kesişir ve üçlü veya daha fazla kavşak yoktur, bu nedenle üç seçimden herhangi biri her zaman bir üçgen verir,” diyor Mangahas. Ona gönderdiğim resimde, bazı çizgiler paralel, bu yüzden aynı üçgenin parçası olamazlar. “Aynı yedi çizgiyi alıp biraz salladıysanız, büyük olasılıkla [Loh’un] sorunu gibi iniyor ve daha fazla üçgen ve benzer sevimli bir cevabın olacak. ”(Kayıt için: 35.)
Whew. Bu yeni üçgen sorununu henüz iş arkadaşlarımla paylaşmadım. Ama keşfetmeden önce sadece bir zaman meselesi - ve biraz daha tartışmak.
🚨ÖNEMLİ GÜNCELLEME 1/30/20Story: Bu hikayeyi yayınladığımızdan beri, çoğu, çok okuyucular, 18'in bu soruna gerçekten kabul edilebilir bir cevap olmasına rağmen, bir tek bir, benim tarafımdan kasıtsız bir gözetim nedeniyle. Üçgeni düz, beyaz bilgisayar kağıdına çizmiş olsaydım, okuyucularda bunu çok daha kolay hale getirebilirdim - ve en önemlisi gelen kutumda çok daha kolay olabilirdim. Ama hayır.
Ne yazık ki bu üçgeni çizgili kağıda çizdim ve birçok akıllı insan doğru bir şekilde işaret etti, aslında, işaretleyicide yazılan koyu mavi çizgilere ek olarak görüntüdeki açık mavi paralel çizgileri sayarsanız, aslında burada toplamda 18'den fazla üçgen vardır - çok daha fazla. Asla sadece bu koyu mavi çizgileri kullanmayı belirtmedim ve bu yüzden yanılıyorum. Haklısın.
Bir okuyucu, Ralph Linsangan, teknik olarak bulunan her ek üçgeni işaretlediği ve toplamda 35 ek 17 üçgen işaretlediği bu görüntüyü göndererek bana tamamen sahip oldu. Seyretmek:
Bu tür bir bağlılık sevdiğim birçok nedenden sadece biri Popüler Mekanik okuyucular. Sizi aşacak bir şey bulamıyoruz arkadaşlar. Bir sonraki teaser'a kadar!
🚨EVET BİR ÜÇGEN GÜNCELLEME 1/31 / 20🚨 YET: Son güncellemeyi yayınladığımdan beri, Daha senin, olası ek üçgenleri düşünmediğim için beni ve okur arkadaşlarınızı gizlemeye devam edin. 45 üçgen olduğunu gösteren başka bir grafikte gönderilen okuyucu Derek Schneider'den haber alalım.
Bununla birlikte, orijinal kuralları takip edersem, kesin ve yeşil olan ve ek olabilecek 9 tane sayıyorum üst köşeyi görsel olarak nasıl yerleştirdiğinize bağlı olarak yoruma açık olun (mor renkte)… Şahsen sayırım o.
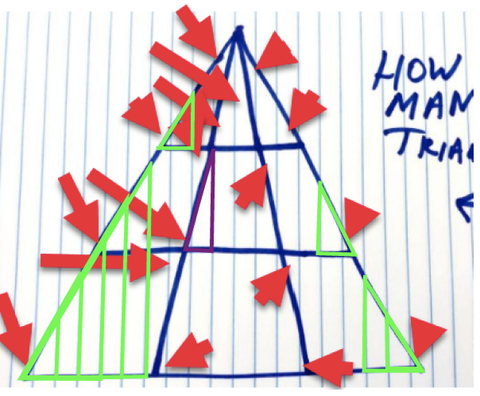
Derek Schneider
Bu arada Reader Poingly, üçgenleri saymak için “ciddi bir hata” yaptığımızı söylemek için yazdı:
Örneğin sağ alt köşeyi ele alalım, bir üçgen için bir ok gösteriyor. Bununla birlikte, bu açık mavi çizgiler tek başına bu köşede üç kadar üçgen oluşturabilir:

Poingly
Bunlardan bazıları biraz tartışmalı olabilir (yani, TAMAMEN açık mavi çizgilerin karanlık olanlarla kesiştiği ve teknik olarak bir üçgen veya dörtgen oluştururlar), bu konuda yapılabilecek YEDİ EK üçgen saydım yol. Bu, toplam üçgen sayısını 42'ye çıkarır.
Kötü haber şu ki bazı üçgenleri kaçırdık. İyi haber şu ki, bu, tam sayı ile kanıtlandığı gibi, hayatın açıkça bir anlam ifade ettiğini teyit ediyor: 42.
Üstün nokta, Poingly. Okuyucu James Goodrich bir adım daha attı ve bir üçgenin ne olabileceğini düşünmek için aklımızı açtığımızı gösteriyor:
Okuyucunuza göre, 17 ek üçgen daha işaret eden ("Andrew hangi çizginin bir üçgenin "yan tümcesinin 3 kenarını içerebileceğini belirtin), açıkça çok fazla bulamadı Daha. Örneğin, 30 Ocak 2020 "Önemli Güncelleme" ekindeki sol alt mini üçgeni ele alalım. Mini üçgenin alanları ve ona bitişik eşkenar dörtgen alanı bir arada başka bir üçgen oluşturmaz mı?
Dikkate alınması gereken başka bir fikir: Üçgenlerin 3 açısı vardır (kim tahmin ederdi?); ancak bir açıyı nasıl tanımladığınızı, bu açılarla farklı üçgenler oluşturacağını varsayıyorum. A, B ve C köşeleri olan bir üçgen T verildiğinde, t-one ABC tarafından açıklanabilir, B merkezi açıdır. BAC tarafından tarif edilen t-ikisinin farklı olduğunu öneririm. Benzer şekilde BCA için.
Daha sonra belirli bir durumu, dik açılı üçgenleri alırsak, sinüs, kosinüs ve teğet fonksiyonlarını (SOH, CAH, TOA) türetebiliriz. Bunu üçgene uygularsak (ve dik açı gereksinimini gevşetirsek, BAC'nin CAB'dan farklı olduğu anlamına gelebilir. Tabii ki, izoskol ve eşkenar üçgenler için istisnalar yapılır (ikincisi sadece 3 farklı üçgen tanımına sahip olacaktır).
Her bir öneriyi nasıl ölçeceğimizi tam olarak düşünmedim (ve ikincisini sonra uygulamak, sayıyı artıracaktır) yine de), bu nedenle güncellenmiş önemli bir güncellemede kullanmanız için kolay bir numaram yok (fikirlerimi buna değer bulursanız) Güncelleme).
Yaptım, James. Ve bekleyeceğim. Begrudgingly, yeni kaotik kurallarımıza kaç tane ek üçgen verilebileceğini bulmak için son bir bıçak almaya karar verdim ve 43'e geldim ve toplamda 61:
Andrew Daniels
Bununla birlikte, bunu okuyan birinin çok hızlı bir şekilde yine yanıldığımı söyleyeceğinden ve kanıt sunacağından eminim daha uzun ve dolambaçlı yoldan başka bir tavşan deliğinden geçerek delilik. (Yan not: Eşimi üç gündür görmedim. Lütfen ona onu sevdiğimi söyle.) Bu yüzden son bir zorluk çıkarıyorum: Orijinal görüntüde en olası üçgenleri bulabilirseniz, bana çalışmanızı gösterin ve kesin olarak kanıtlayın üstünlüğünüz varsa, bu hikayeyi son bir kez güncelleyeceğim ve şimdi Üçgen Kral veya Kraliçe'yi taçlandıracağım, şimdi ve sonsuza dek. Yolunuz açık olsun.

SpeedRipper Rubik Küpü
$12.45
Rubik küpü 40 yıldır insanları çıldırtıyor. Kendiniz anlamaya çalışın veya nasıl çözeceğini öğren matematik kullanarak.

Kanoodle 3 Boyutlu Bulmaca Oyunu
$8.79
Sadece 12 parça ancak toplam 200 zorluk ile Kanoodle, hem çocukları hem de yetişkinleri 2-D ve 3-D bulmacalarla güdük.

Sagrada Masa Oyunu
$29.98
En iyi bulmacalardan birinde yılın masa oyunları, siz ve diğer üç oyuncu Sagrada Familia'nın vitray pencerelerini yapmaya çalışıyorsunuz.

Boyut 3 Boyutlu Bulmaca Oyunu
$40.97
Bu hızlı tempolu 3-D bulmaca oyunu hızlı puan, mantık ve şans bir arada en fazla puan kazanmak için küreler yığını içerir.
Gönderen:Popüler Mekanik


